Mathematics

Back

Mathematics Curriculum Intent

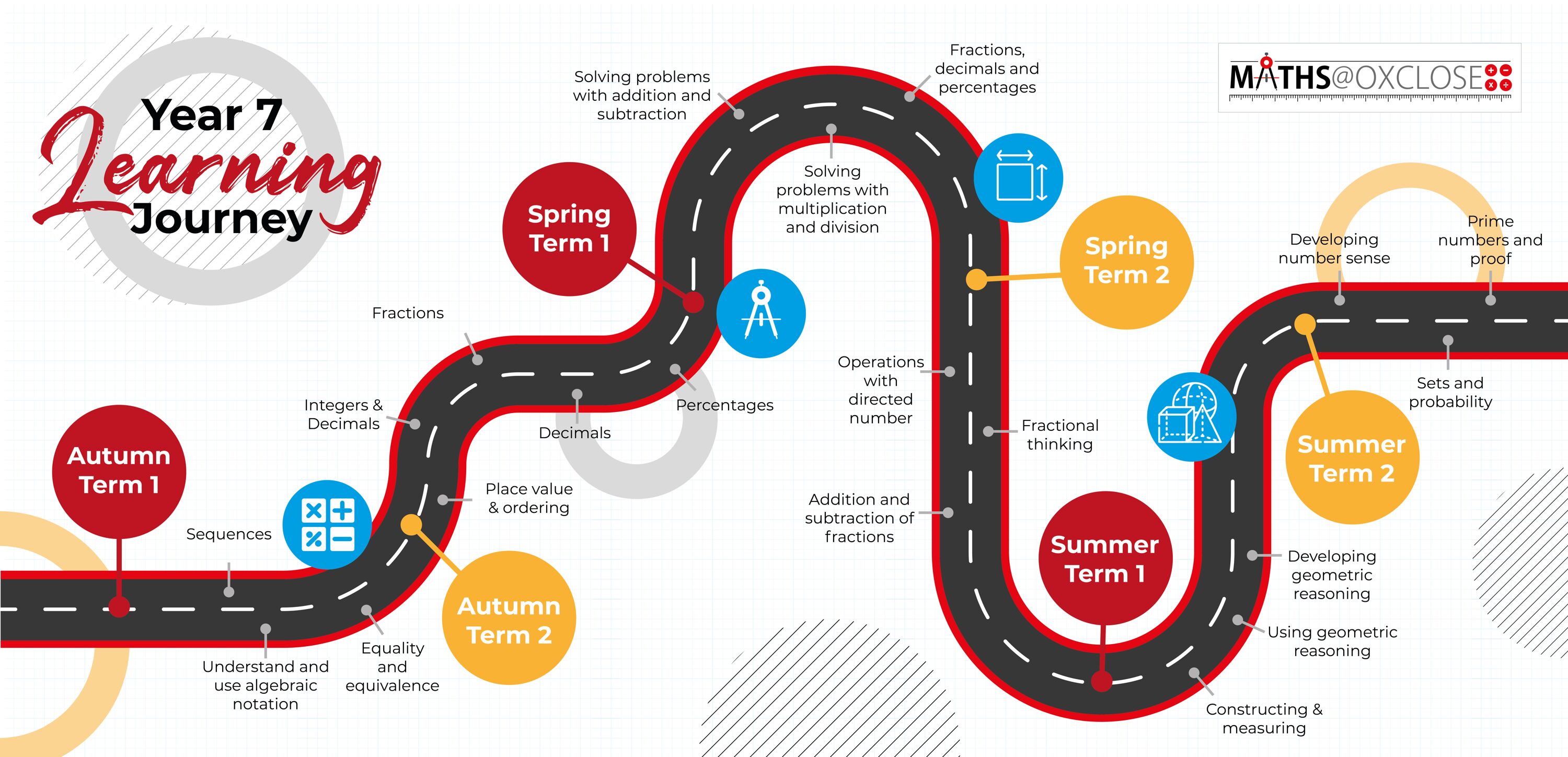
Maths Year 7 Maths Learning Journey

Click to download the Year 7 Maths Learning Journey

Maths Year 8 Maths Learning Journey

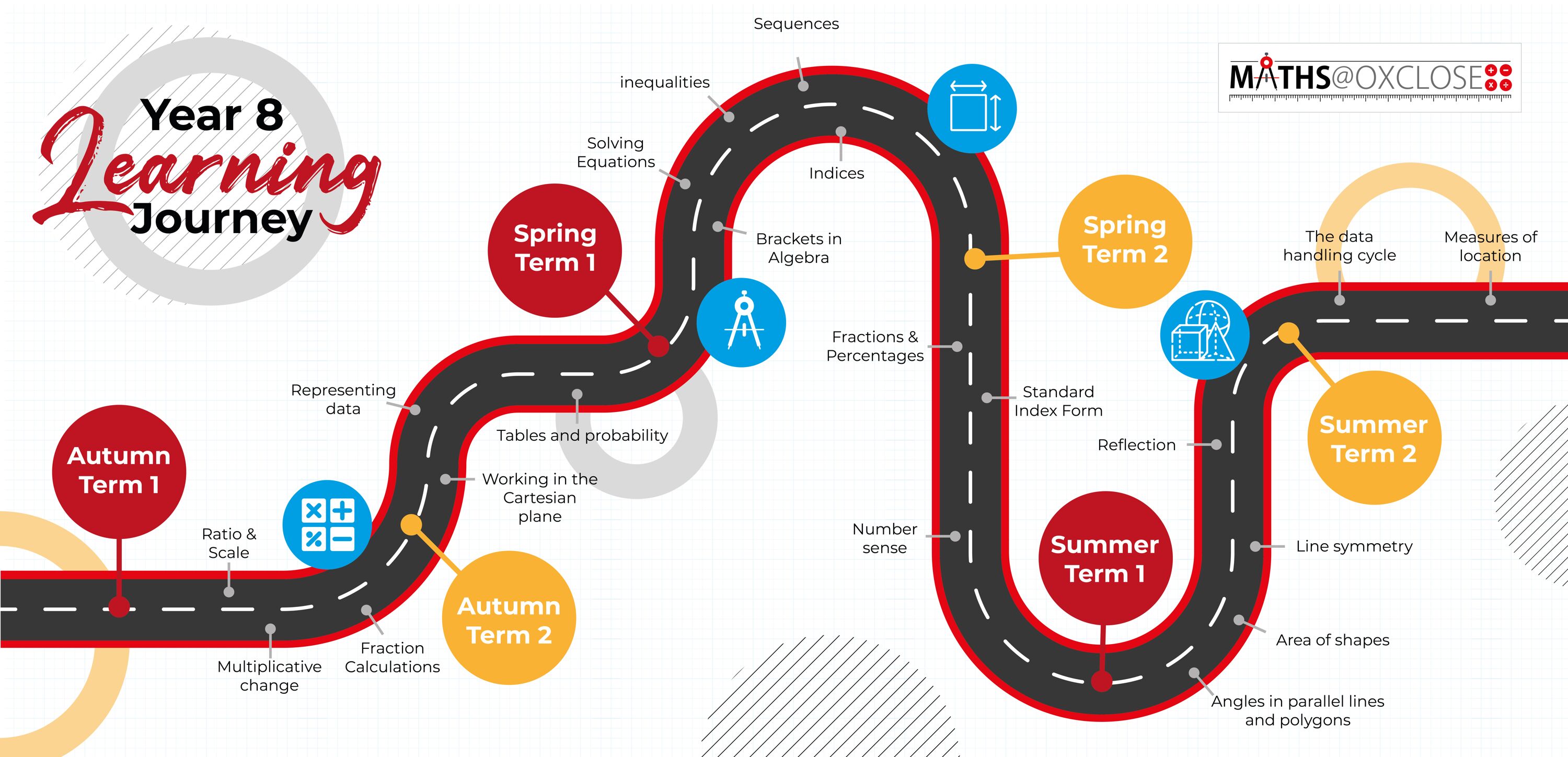
Click to download the Year 8 Maths Learning Journey

Maths Year 9 Maths Learning Journey

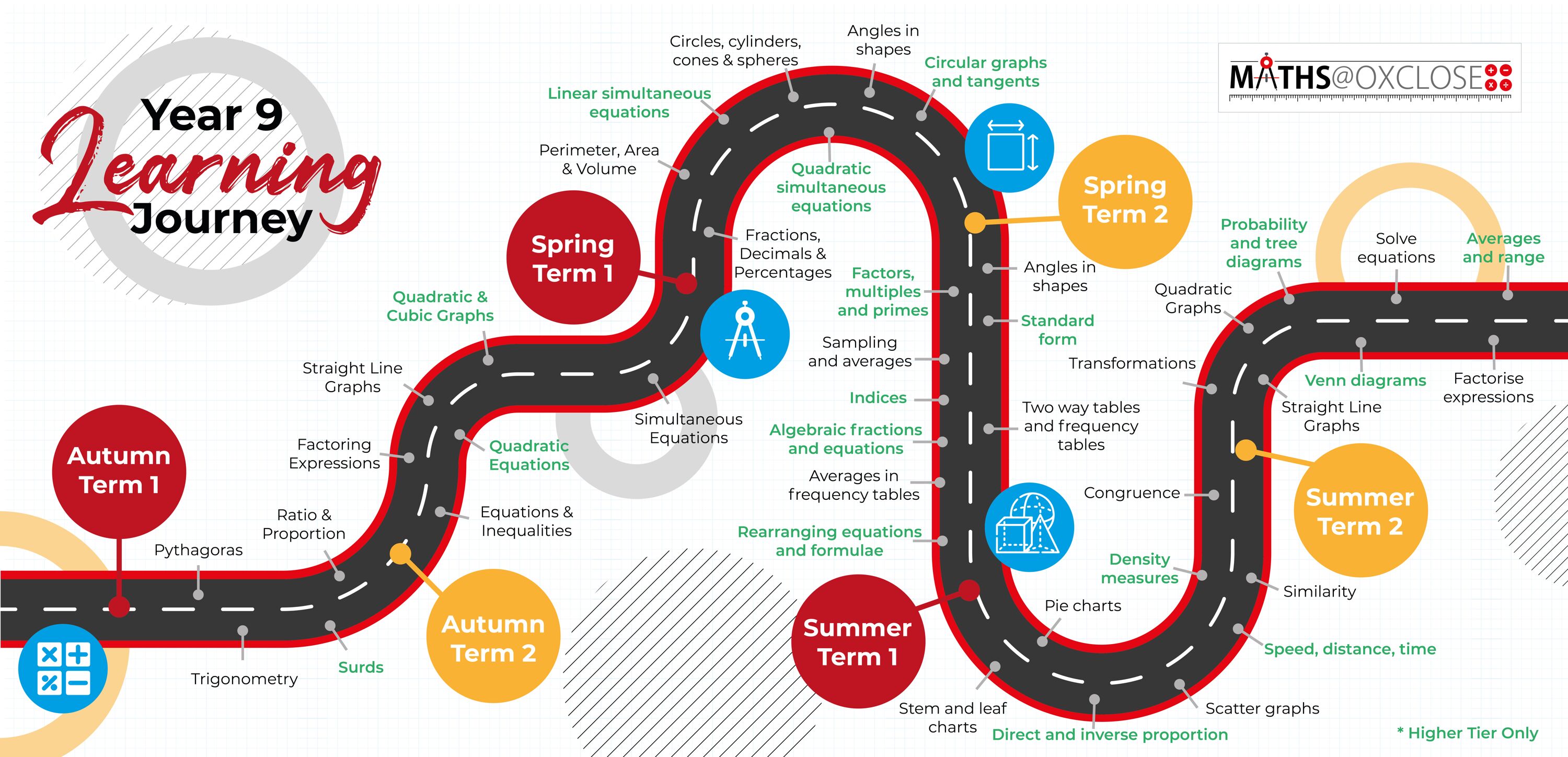
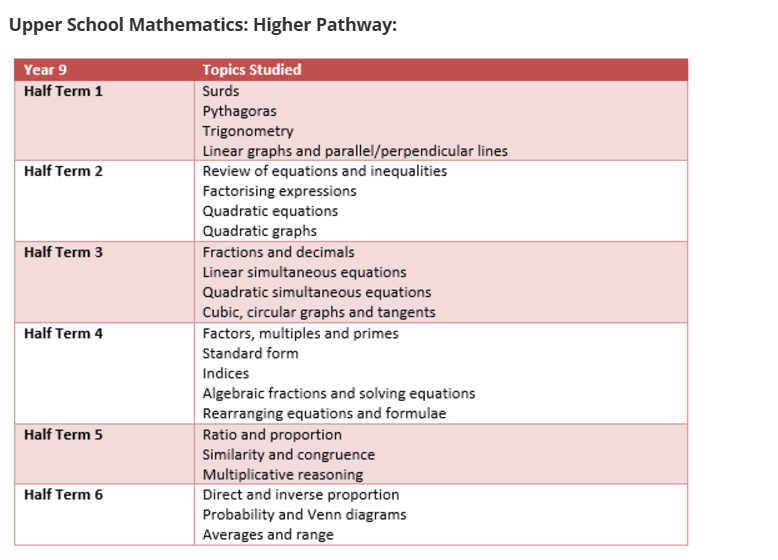
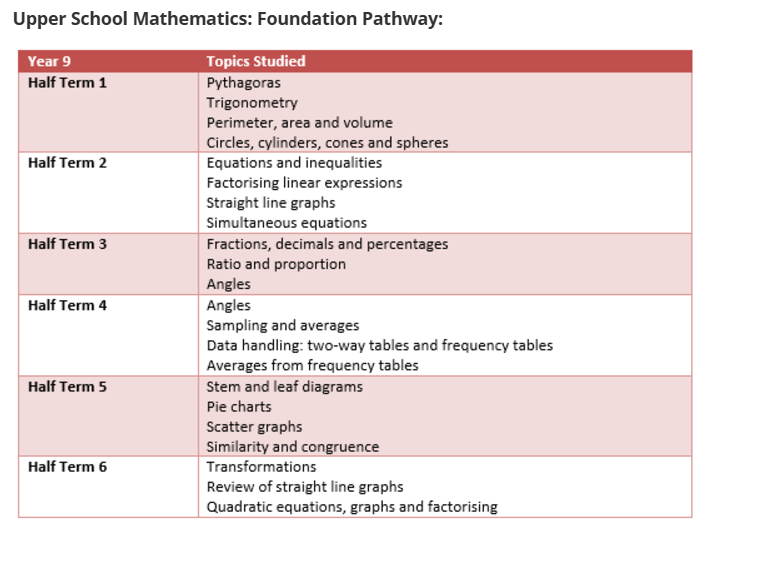
Click to download the Year 9 Maths Learning Journey

 

Maths Year 10 Maths Learning Journey

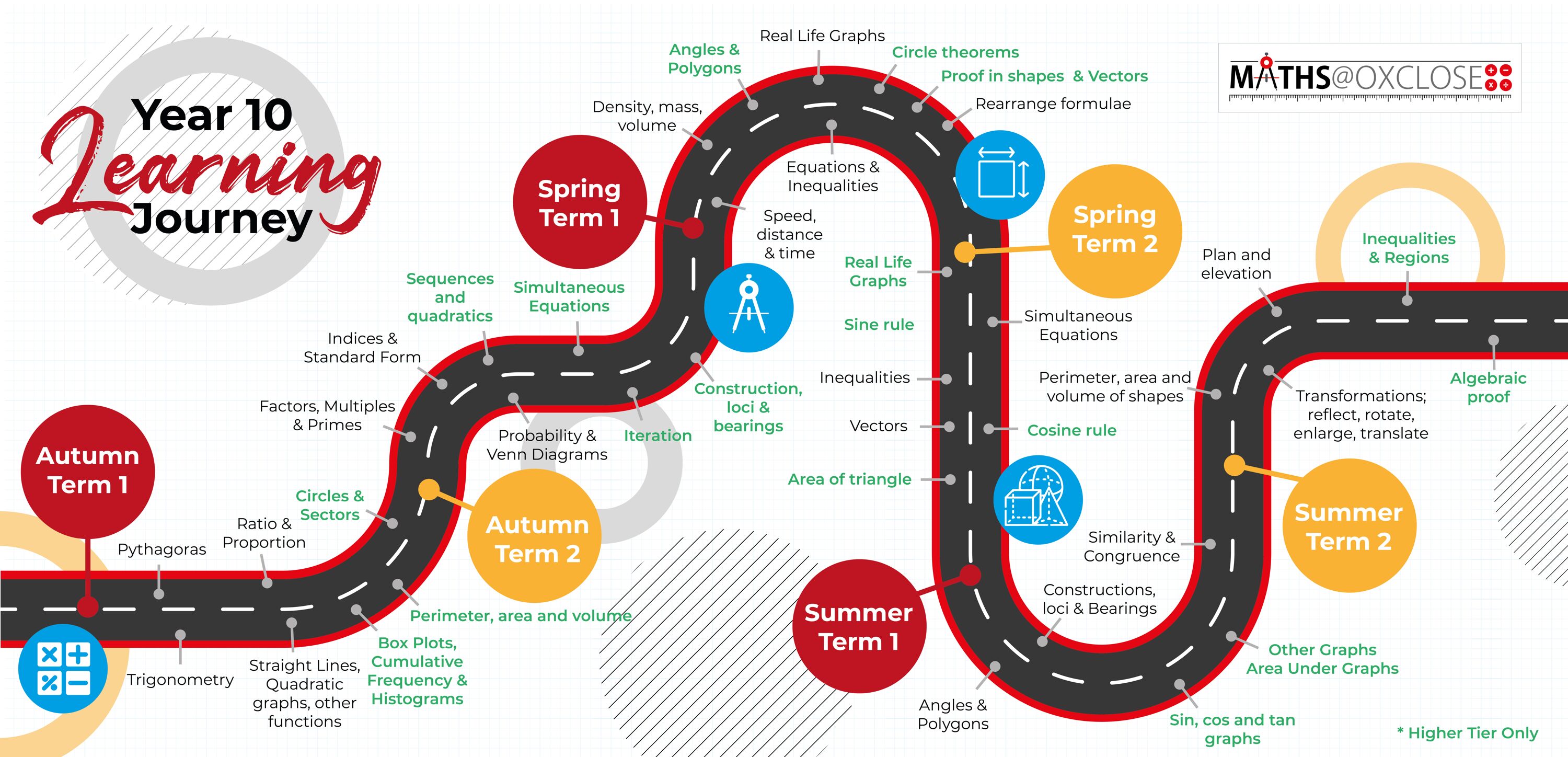
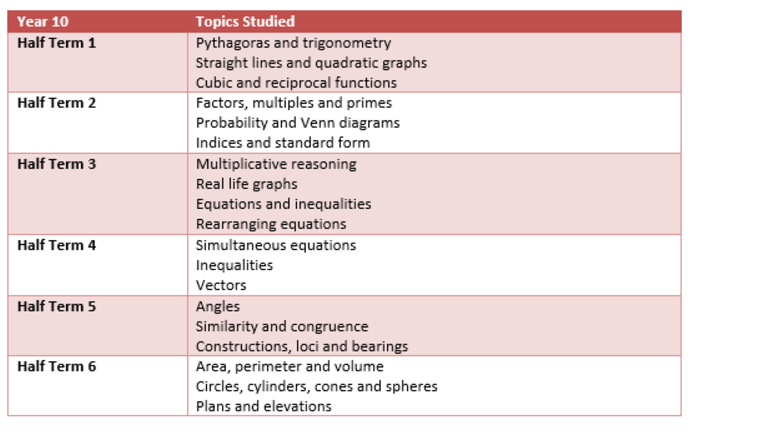
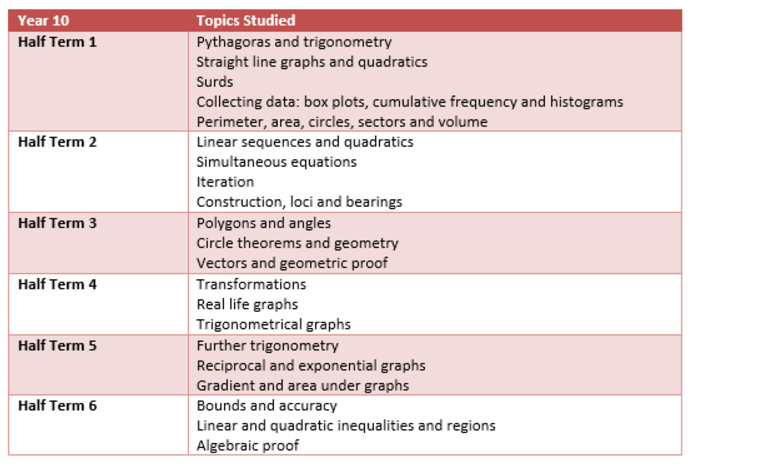
Click to download the Year 10 Maths Learning Journey

 

Maths Year 11 Maths Learning Journey

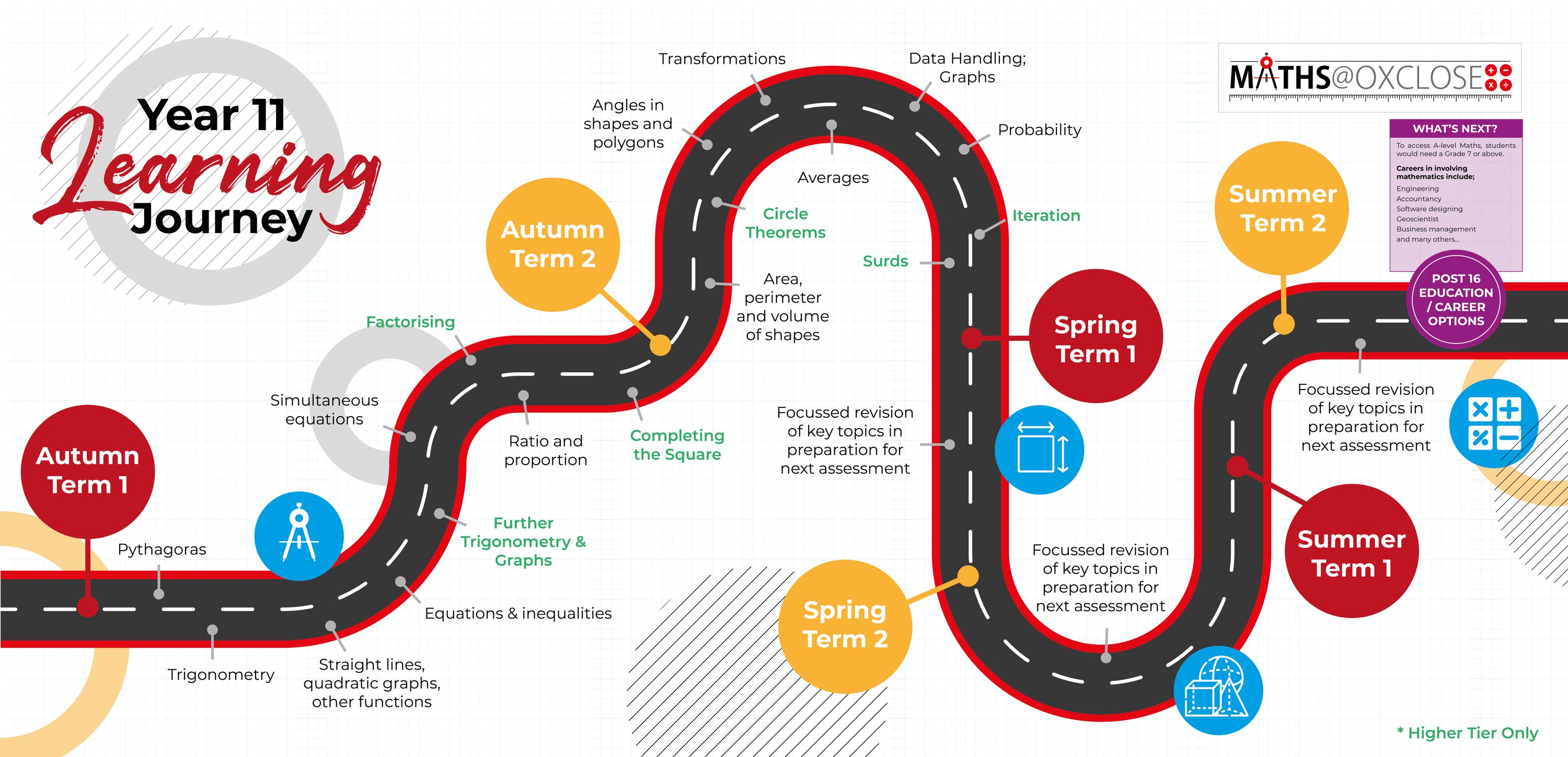
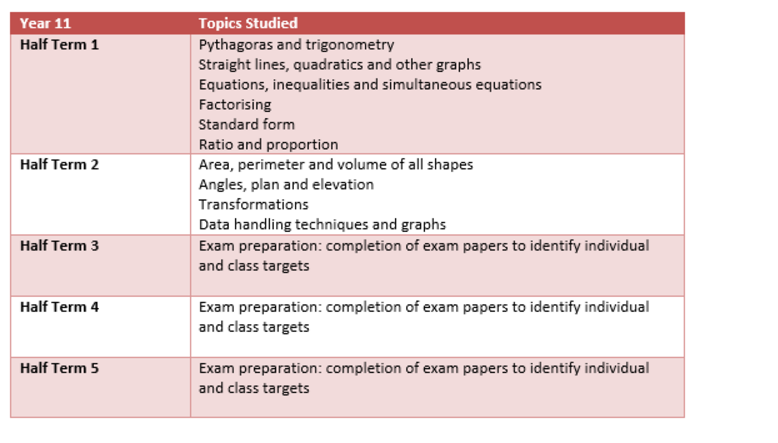
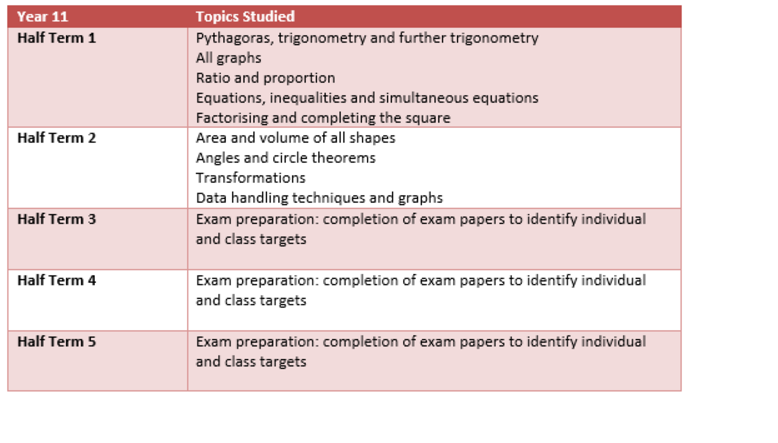
Click to download the Year 11 Maths Learning Journey

 

 

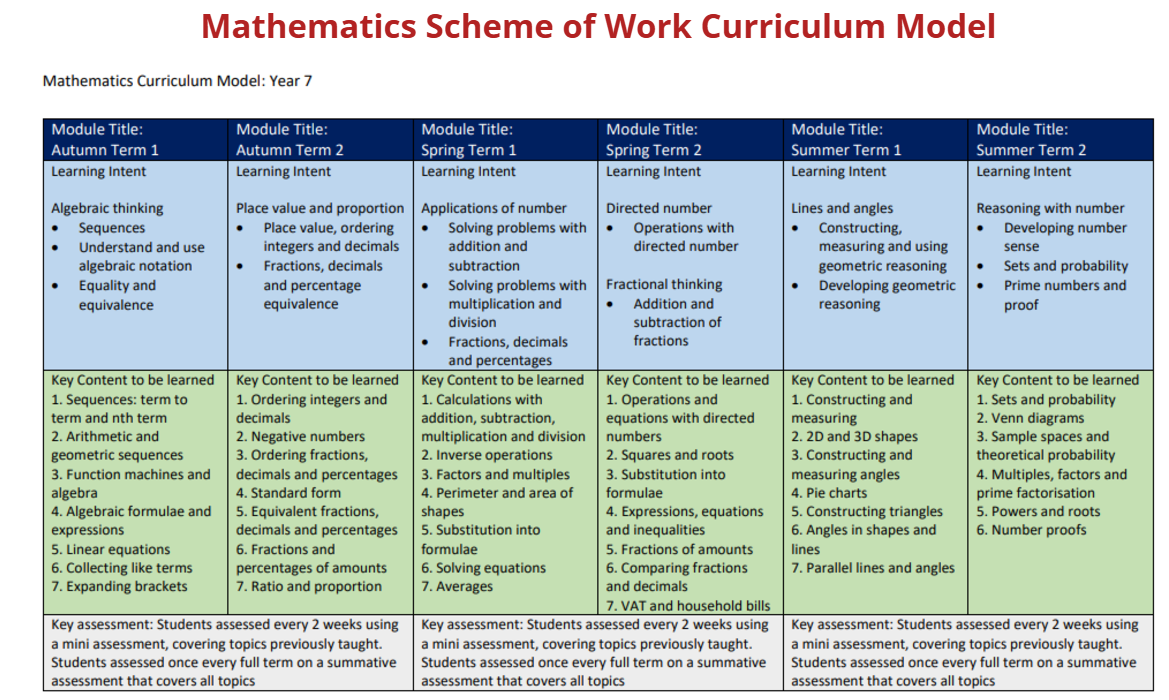
MATH SOW

Click here to download the full Mathematics Scheme of Work Curriculum Model - by year / module / unit

 

 

Year 7

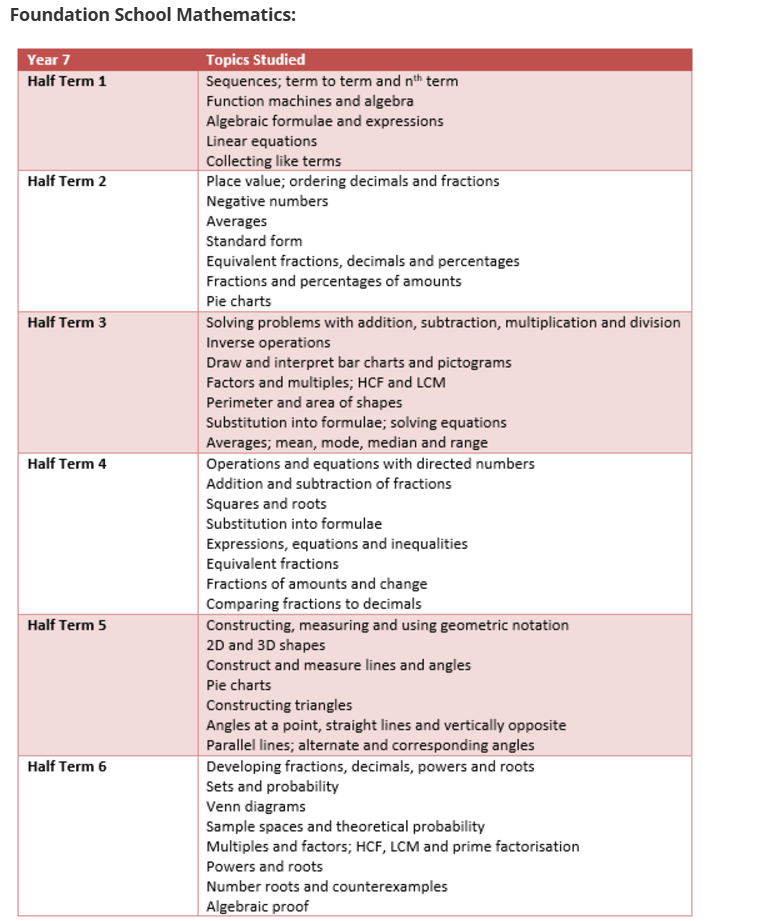
MATH 3

Year 8

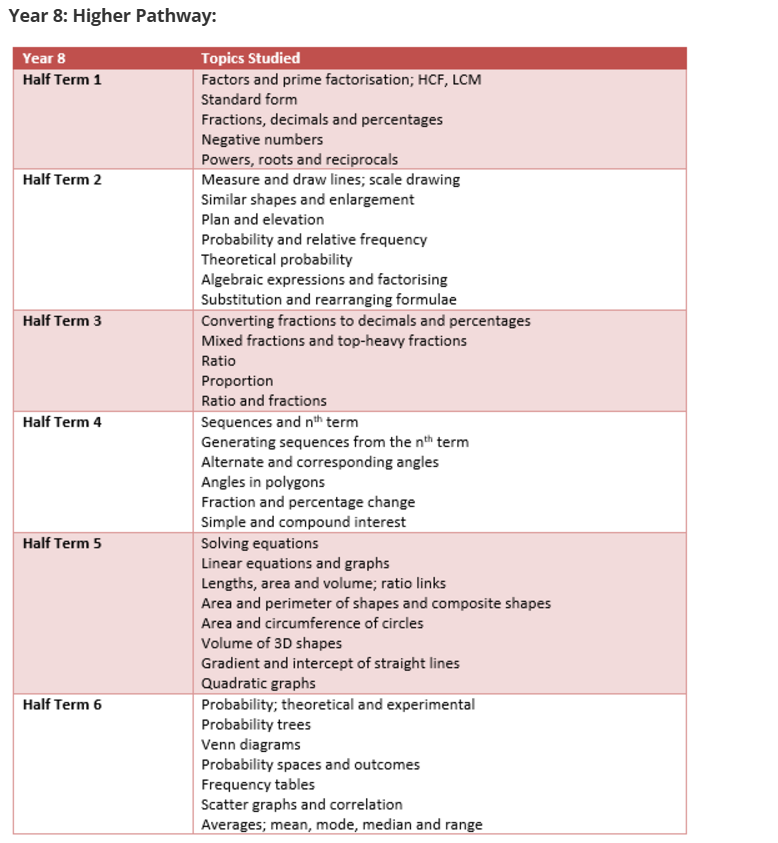
MATH 4

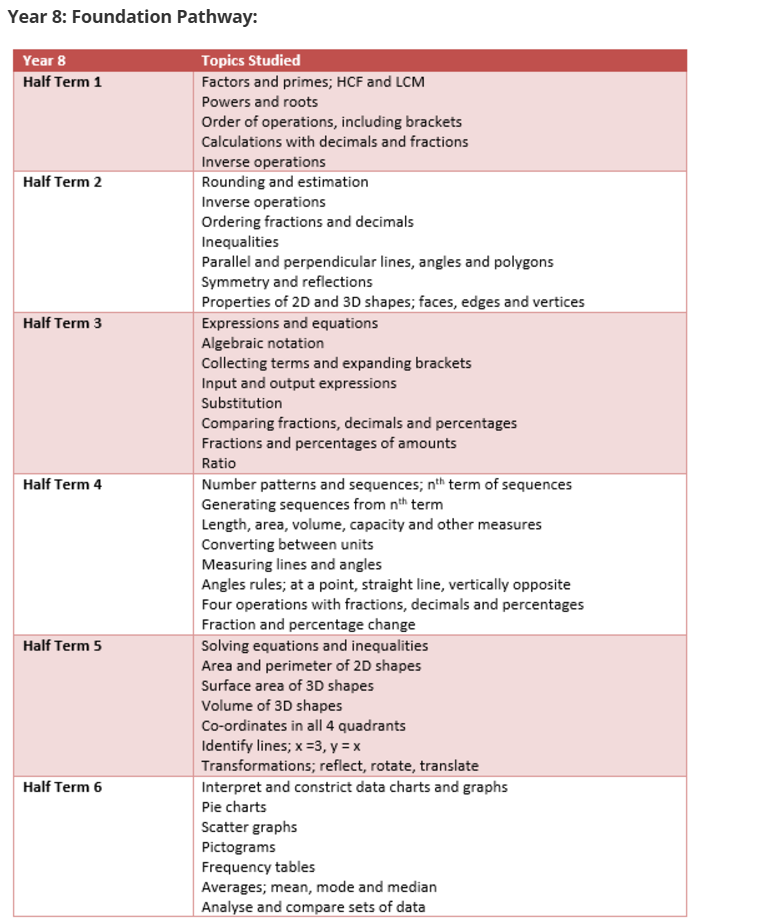
MATH 5

Year 9

MATH 6

MATH 9

Year 10

Upper School Mathematics: Foundation Pathway:

MATH 7

Upper School Mathematics: Higher Pathway:

MATH 10

Year 11

Upper School Mathematics: Foundation Pathway:

MATH 8

Upper School Mathematics: Higher Pathway:

MATH 11